Matemáticas en el imperio sumerio
Nuestro primer conocimiento del uso de la humanidad de las matemáticas viene de los egipcios y de los babilónicos. Ambas civilizaciones desarrollaron de una forma similar, pero también
muy diferente.
Las matemáticas sumerias se desarrollaron inicialmente en gran medida como respuesta a las necesidades burocráticas cuando su civilización se asentó y desarrolló la agricultura
(posiblemente ya en el sexto milenio antes de Cristo) para la medición de parcelas, la tributación de los individuos, etc.
Además, los sumerios necesitaba escribir números bastante grandes mientras intentaban trazar el curso del cielo nocturno y desarrollar su sofisticado calendario lunar.
Quizás fueron las primeras personas en asignar símbolos a grupos de objetos en un intento de facilitar la descripción de números mayores.
Pasaron de utilizar símbolos o símbolos separados para representar gavillas de trigo, jarras de aceite, etc., hasta el uso más abstracto de un símbolo para números específicos
de cualquier cosa.
Comenzando ya en el cuarto milenio antes de Cristo, comenzaron a usar un pequeño cono de arcilla para representar uno, una bola de arcilla para diez y un cono grande para sesenta.
A lo largo del tercer milenio antes de cristo, estos objetos fueron reemplazados por equivalentes cuneiformes para que los números pudieran escribirse con el mismo estilete que se
estaba utilizando para las palabras en el texto.
Un modelo rudimentario del ábaco probablemente estaba en uso en Sumeria desde tan temprano como 2700 - 2300 BCE.
El modelo cuneiforme (cuña) de escritura que los Sumerios habían desarrollado durante el cuarto milenio AC pudo haber sido la forma más temprana de comunicación escrita. Este
modelo, es anterior al jeroglífico egipcio.
El uso de la escritura cuneiforme fue muy utilizado. Las leyes, cuentas de impuestos, historias, lecciones de la escuela, las cartas personales fueron impresionadas en las tablillas suaves de la arcilla y
después cocidas al calor del sol o en hornos.
Solo a partir de una región, el sitio de Nippur antiguo, se han recuperado unas 50.000 tablillas.
Muchas bibliotecas de la Universidades en todo el mundo tienen colecciones de tablillas cuneiformes.
La clave para descifrar la escritura cuneiforme fue una inscripción trilingüe. Encontrada en Behistun por una expedición británica dirigida por; Henry Rawlinson (1810-1890),
representa la grandeza y gloria de Dario el grande.
Como la piedra de Rosetta, estaba escrita en tres lenguajes -- Viejo Persa, Elamita, y Acadio (babilónico). Sin embargo, los tres lenguajes eran desconocidos.
Solamente porque el viejo persa tiene solamente 43 signos y había sido el tema de serias investigaciones alrededor del principio del siglo diecinueve se logró descifrar.
No obstante, el progreso fue muy lento.
Gracias a esta inscripción trilingüe, Rawlinson pudo correctamente asignar los valores correctos a 246 caracteres y descubrió que el mismo signo podría representar
diversas consonantes, dependiendo de la vocal que la seguía (polifonia).
En este documento no haremos distinción entre matemática sumeria (anterior a 1800 AC) y paleobabilónica, ya que incluiremos referencias a tablillas de 1700 AC (babilónicas).
Ya que es practicamente la misma fuente y método el que usaron ambas civilizaciones.
MATEMATICAS
En matemáticas, los sumerios eran más avanzados que los egipcios.
Notación matemática
Para la notación matemática los sumerios a partir del tercer milenio A.C , con el desarrollo de la escritura cuneiforme, utilizaron dos símbolos. Uno para representar la unidad y otro para representar la decena.
el símbolo 1 equivale al UNO (1) y el símbolo : equivale al DIEZ (10)
Todos los números , enteros o fracciones eran representados por estos dos símbolos:
Ejemplo:
= 7 equivale 47
Observe que la notación era posicional y sexagesimal: o sea que cada unidad en una posición a la izquierda equivalía a 60 unidades en la posición derecha
Ejemplos:
; ; equivale a: 20 x 60 + 20 = 120
2 2 11 equivale a : 2 x 60 2 + 2 x 60 + 11 = 7.331
No hay razón clara por la que se conozca porque los sumerios seleccionaron el sistema sexagesimal. Fue seleccionado posiblemente en el interés
de la metrología, ésta es la teoría según Theon de Alexandría, comentarista del cuarto siglo D.C. que se apoya en que los valores 2.3.5.10.12.15.20 y 30 todos ellos dividen 60.
Por esta razón resulta rápido y cómodo realizar particiones. Además, los números grandes exigen menos cifras para representarse; por ejemplo, el número 216.000 en base 10 se representa como 1.000 en base 60.
Aunque hay otras teorías como la del historiador asiriólogo G. Kewistch (1.904) o el matemático Georges Ifrah (1.947-) que suponen el origen a la fusión de dos culturas con diferentes sistemas de numeración. (decimal y base 6 o 12 )
Los remanentes de este sistema de notación numérica que todavía existen hoy son tiempo y las medidas angulares. De hecho los sumerios utilizaron relojes de 12 horas dobles, con 60 minutos y 60 segundos y su año civil constaba de 360 días.
En este sistema de notación se detecta un incidente posicional.
Por ejemplo si vemos en una tablilla representados dos veces el símbolo del DIEZ : :
Esto puede tener diferentes significados como:
= 10 x 60 + 10 = 70
= 10 x 60 2 + 10 x 60 = 36.600
hasta puede ser = 20
Ya que no hay designador de situación para saber donde empiezan las unidades, y aunque hay una coma flotante verdadera -- su localización
es indeterminada excepto si analizamos el contexto, y en algunas ocasiones puede llevar a confusión.
En los ejemplos que tendremos, usaremos la coma (,) para separar las posiciones de los números y el punto y coma (;) para separar la parte entera de la decimal o fraccionaria.
Esta es la notación que realizó el investigador Otto Neugebauer [4].
Asi la secuencia :
"d1 ; d2 , d3, d4 ..... " equivaldrá a
d1
+ d2/60
+ d3/602
+ d4/603
+ ....
Siendo los valores d1 d2 d3 d4 ... números enteros.
Ejemplo:
En una vieja tablilla sumeria (colección de fechada entre 1900 AC y 1800 AC) se encontró el siguiente número:
1 ;4 ;<1 :
Los valores corresponderían a la secuencia :
1;24,51,10 que equivale a
1
+ 24/60
+ 51/602
+ 10/603
= 1,41421296
√2
El valor exacto de
√2
con 8 decimales es = 1,41421356.
En el apartado de Pitágoras y medidas triangulares, volveremos con esta interesante tablilla de Yale #7289.
F Ir al inicio de la página
Fracciones.
Las fracciones usadas eran las de denominador 60 o multiplo, como:
7/60
,
21/602
,
30/603
, ....
porque era la expresión sexagesimal era conocida.
Debido a la divisibilidad del 60 podían obtener facilmente fracciones como:
Usando la expresión ;30 que se representaba como <
Usando la expresión ;20 que se representaba como ;
Usando la expresión ;15 que se representaba como :5
Usando la expresión ;12 que se representaba como :2
Usando la expresión ;10 que se representaba como :
Usando la expresión ;6 que se representaba como 6
También podían usar otras fracciones como:
Usando la expresión ;7,30 que se representaba como 7 <
Usando la expresión ;6,40 que se representaba como 6 =
Estas fracciones representan los inversos o reciprocos. Los sumerios utilizaban los inversos o reciprocos para solucionar diversos problemas de cálculo, por esta razón se han encontrad muchas
tablillas con listas de inversos, ya que eran habituales en las escuelas o como herramientas de cálculo.
Fracciones irregulares tales como:
1 /7
o
1 /11
o
1 /13
etc..., no se utilizan generalmente.
Se ha encontrado muchas tablillas con la lista de reciprocos/inversos, o lo que es equivalente ,los pares de factores de sesenta.
Tablilla ERM 14645
Museo de St. Petersburgo
(1900 - 1600 AC)
inverso de 2
inverso de 3
inverso de 4
inverso de 5
inverso de 6
inverso de 7;30
inverso de 8
inverso de 9
inverso de 10
inverso de 12
inverso de 15
inverso de 16
inverso de 18
inverso de 20
inverso de 24
inverso de 25
30
20
15
12
10
8
7;30
6;40
6
5
4
3;45
3;20
3
2;30
2;24
Tablilla MS 3874
Colección Schøyen.
[8]
inverso 1;30
inverso de 2
inverso de 3
inverso de 4
inverso de 5
inverso de 6
inverso de 8
inverso de 9
inverso de 10
inverso de 12
inverso de 15
inverso de 16
inverso de 18
inverso de 20
inverso de 24
inverso de 25
...
40
30
20
15
12
10
7;30
6;40
6
5
4
3;45
3;20
3
2;30
2;24
...
Los sumerios , aunque no utilizaban fracciones irregulares,en algunos casos realizaban algunas aproximaciones:
1 /59
= ; 1,1,1 1 /61
= ; 0,59,0,59
F Ir al inicio de la página
Multiplicación y división.
Se han encontrado numerosas tablillas con tablas de multiplicar.
Las tablas de multiplicar representaban una dificultad para los sumerios, ya que al tener 60 números necesitaban conocer 60 tablas de 60x60.
Por eso al inicio realizaron tablillas para representar todas las tablas de multiplicar
Tablilla MS 3866 -- Colección Schøyen.[8]
Esta es un tablilla curiosa ya que representa la tabla de multiplicar del número del número 1;12 equivalente al 1,2 (decimal), este número es el recíproco de 50,
lo que demuestra que no sólo tenían tablas de mutiplicar de valores enteros. También curiosamente termina con el valor de cuadrado de 1;12.
Anverso
| 1;12 | 1 | 1;12 |
| 2 | 2;24 |
| 3 | 3;36 |
| 4 | 4;48 |
| ... | ... | ... |
| 16 | 19;12 |
Reverso
| 17 | 20;24 |
| 1;12 | 3 | 3;36 |
| 1;12 | 4 | 4;48 |
| ... | ... | ... |
| 50 | 1 |
| 1;12 | 1;12 | 1;16;24 |
Manejar tantas tablillas para multiplicar era engorroso por lo que para realizar la multilicación los sumerios indistintamente una de estas dos fórmulas:
a· b= (a+b)2- (a-b)2/4
a· b= (a+b)2 - a2 -b2/2
Así utilizaban tablas de cuadrados, y aplicando una de las dos formulas se hacía mucho más facil realizar las multiplicaciones
En Tell al Senkareh (Antigua Larsa) se encontraron un conjunto de tablillas fechadas en el 2000 a.c. que dan los cuadrados de los
números hasta 59 y de los cubos hasta 32.
La división se asimiló a la multiplicación, es decir:
y para ello utilizaban las tablas de inversos.
F Ir al inicio de la página
Las raíces cuadradas
Normalmente para extraer las raices cuadradas o cúbicas, utilizaban las tablas de cuadrados o cubos ya mencionadas, o de raíces cuadradas.
Tablilla CBS 08266
Museo de Antropología de la Universidad de Pennsylvania
Tablilla de raices cuadradas, datada entre 1900 ac y 1600 ac.
Encontrada en Nippur
Muestra los cuadrados de los números 30 a 40, o si se prefiere las raices cuadradas
15,0;
16,1;
17,4;
...
30;
31;
32;
...
asi pues:
√15,0; = 30 ya que 15,0; (sumerio) es 900 (decimal)
√16,1; = 31 ya que 16,1; (sumerio) es 961 (decimal)
√17,4; = 32 ya que 17,4; (sumerio) es 1024 (decimal)
Para calcular y realizar estas tablillas se supone que podrían utulizar alguno de estos métodos:
- TEORIA 1: Aplicación de la aproximación:
Desarrollado por David Fowler and Eleanor Robson [1]
- TEORIA 2: Aplicación del método de la media.
Se realiza por iteraciones, partiendo de un valor inicial a1 (que se aproxima o intuye, normalmente llamado semilla), se sustituye dicho valor en la formula obteniendose como resultado
a2 y dicho valor se vuelve a introducir en la formula como valor inicial. Este proceso se repite tantas veces como sea necesario.
Siendo N el valor del que deseamos obtener la raiz cuadrada.
Puede probarse este método en el proyecto del MIT https://scratch.mit.edu/projects/45120106/
Nota 1: Aunque como ya hemos visto en la tablilla YALE #7289, tenían un valor de
√2
equivalente a 1;24,51,10, a efectos de cálculo usaban frecuentemente como aproximación el valor 1;25 que es igual a 1,4166
Nota 2: En la tablilla W 1923-366 se muestra en dos columnas la secuencia raices cuadradas :
1;2,1
1;4,4
1;6,9
1;8,16
1;10,25
...
1;1
1;2
1;3
1;4
1;5
...
Aun estando en notación sumeria, la similitud con las raices de los números decimales 121, 144, 169, 189, 225 es sorprendente.
Ello es debido a que, utilizando la notación de Otto Neugebauer[4], la igualdad: (1;1)2 = 1;2,1 con la base del sistema de numeración mayor que 2.
Lo mismo pasa con (1;2)2 = 1;4,4 y sucesivas.
F Ir al inicio de la página
El descubrimiento de la tablilla de Plimpton 322, cerca de Tell Senkereh (antigua Larsa) fechada hacia 1800 A.C. nos indica que los sumerios conocían la relación pitagórica de los lados de un triángulo rectángulo.
Teorema de Pitágoras
Este conocimiento es básico para un agrimensor, que desea realizar parcelar con angulos rectos en un terreno o para un constructor que desea hacer paredes perpendiculares, ya que con una
simple soga, conociendo la relación pitagórica 3, 4 y 5 pueden hacerse estas labores.
Tablilla Plimptom 322 . Universidad Columbia.


Esta tablilla [2][3] [5] tiene una serie de números tabulados,
| (1:)59:00:15 | 1:59 | 2:49 | 1 |
| (1:)56:56:58:14:50:06:15 | 56:07 | 1:20:25 | 2 |
| (1:)55:07:41:15:33:45 | 1:16:41 | 1:50:49 | 3 |
| (1:)53:10:29:32:52:16 | 3:31:49 | 5:09:01 | 4 |
| (1:)48:54:01:40 | 1:05 | 1:37 | 5 |
| (1:)47:06:41:40 | 5:19 | 8:01 | 6 |
| (1:)43:11:56:28:26:40 | 38:11 | 59:01 | 7 |
| (1:)41:33:45:14:03:45 | 13:19 | 20:49 | 8 |
| (1:)38:33:36:36 | 8:01 | 12:49 | 9 |
| (1:)35:10:02:28:27:24:26 | 1:22:41 | 2:16:01 | 10 |
| (1:)33:45 | 45 | 1:15 | 11 |
| (1:)29:21:54:02:15 | 27:59 | 48:49 | 12 |
| (1:)27:00:03:45 | 2:41 | 4:49 | 13 |
| (1:)25:48:51:35:06:40 | 29:31 | 53:49 | 14 |
| (1:)23:13:46:40 | 56 | 1:46 | 15 |
Convertimos esta tabla a notación decimal y obtenemos los valores para estas 4 columnas:
1,9834
1,9492
1,9188
1,8862
1,8150
1,7852
1,7200
1,6928
1,6427
1,5861
1,5625
1,4894
1,4500
1,4302
1,3872
119
3367
4601
12709
65
319
2291
799
481
4961
45
1679
161
1771
56
169
4825
6649
18541
97
481
3541
1249
769
8161
75
2929
289
32229
106
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
La interpretación de la tablilla:
Otto E. Neugebauer aboga por una interpretación de Teoría de Números, señalando que esta tableta provee una lista de (pares de números que conforman) ternas pitagóricas.
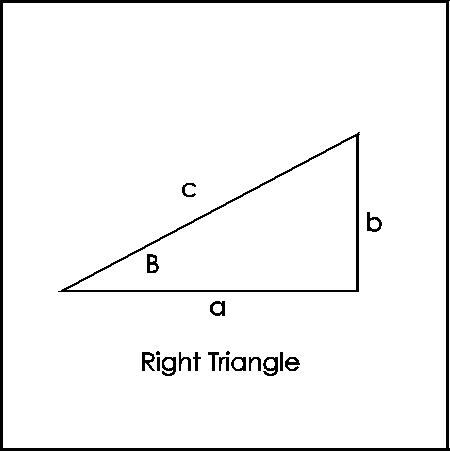
Si consideramos un triángulo rectángulo como el de la imagen, de lados "a" y "b", e hipotenusa "c".
La tablilla nos muestra una tabla con los valores de:
b
120
3456
.
.
.
90
( c/b )2
( 169/120 )2
( 4825/3456 )2
.
.
.
( 106/90 )2
a
119
3367
.
.
.
56
c
169
4825
.
.
.
106
1
2
.
.
.
15
Por tanto, esta tabla da una serie de valores de
"( c/b )2" "a" y "c" que cumplen con ternas pitágorica.
Así le línea 1 representa la terna pitagórica
(120,119,169)
Es interesante, la línea 11 de la tabla :
En notación decimal será:
Si
(b/c)2 = 1,5625 , siendo
c=75 nos da que
b=60, lo que nos porpociona la terna pitagórica
(60,45,75).
Reduciéndolo se puede observar que es un triángulo proporcional al de la conocida terna pitagórica
(3,4,5).
Ahora observemos el reultado de calcular "b" y su valor en notacion sexagesimal sumeria.
| b | a | c | b(sumerio) |
|---|
| 1 | 120 | 119 | 169 | 2,0 |
| 2 | 3456 | 3367 | 4825 | 57,36; |
| 3 | 4800 | 4601 | 6649 | 1,20,0; |
| 4 | 13500 | 12709 | 18541 | 3,45,0; |
| 5 | 72 | 65 | 97 | 1,12; |
| 6 | 360 | 319 | 481 | 6,0; |
| 7 | 2700 | 2291 | 3541 | 45,0; |
| 8 | 960 | 799 | 1249 | 16,0; |
| 9 | 600 | 481 | 769 | 10,0; |
| 10 | 6480 | 4961 | 8161 | 1,48,0; |
| 11 | 60 | 45 | 75 | 1,0; |
| 12 | 2400 | 1679 | 2929 | 40,0; |
| 13 | 240 | 161 | 289 | 4,0; |
| 14 | 2700 | 1771 | 3229 | 45,0; |
| 15 | 90 | 56 | 106 | 1,30; |
Vemos que el resultado "b" es un número corto, siempre múltiplo de 6,y en casi todos los casos de 60.
Se observa una anomalía en la línea 2, parece ser que hubo un error de cálculo, aunque los todos números cumplen la terna trigonométrica.
Se supone que estas tablillas eran usadas por estudiantes y pueden ser que sean las respuestas a unos problemas concretos.
Esto hace suponer que el valor de b, debía ser parte del enunciado del problema, ya que siempre es un numero finito y casi siempre múltiplo de 60,
Hay otra interpretación que hace Neugebauer, de la tablilla Plimptom. Basándose en que si p y q son dos números primos
entonces puede considerarse que ( p2-q2 , 2p·q , p2+q2 ) formarán una terna pitagórica, y todos las ternas pitagóricas se pueden formar
de esta manera o como múltiplos de una terna formada de esta manera.
Por ejemplo, la línea 11 puede ser generada por esta fórmula con p = 1 y q = 2. (ya que estos valores de q generan la terna (3,4,5) que es equivalente a la (45,60,75)
Entonces, sostiene Neugebauer, cada línea de la tabla puede ser generada por un par (p, q) que son a la vez números regulares, divisores enteros de una potencia de 60.
Número Regular: es aquel que es divisible sólo por 2, 3 y 5, o combinaciones de ellos.
Sin embargo, como Eleanor Robson (2002) señala, la teoría de Neugebauer no explica cómo se eligieron los valores de p y q: hay 92 pares de números primos entre sí regulares
hasta el 60, y sólo 15 entradas en la tabla. Además, no explica por qué las entradas de la tabla están en el orden en que aparecen.
Los valores de p y q (en notación decimal), y del ángulo B, para las quince entradas de la tabla:
| p | q | Ángulo B |
|---|
| 1 | 5 | 12 | 45° 14' 23" |
| 2 | 27 | 64 | 45° 44' 50" |
| 3 | 32 | 75 | 46° 12' 45" |
| 4 | 54 | 125 | 46° 43' 43" |
| 5 | 4 | 9 | 47° 55' 29" |
| 6 | 9 | 20 | 48° 27' 19" |
| 7 | 25 | 54 | 49° 41' 05" |
| 8 | 15 | 32 | 50° 13' 46" |
| 9 | 12 | 25 | 51° 16' 55" |
| 10 | 40 | 81 | 52° 33' 46" |
| 11 | 1 | 2 | 53° 07' 48" |
| 12 | 25 | 48 | 55° 01' 26" |
| 13 | 8 | 15 | 56° 08' 41" |
| 14 | 27 | 50 | 56° 44' 17" |
| 15 | 5 | 9 | <58° 06' 33" |
Otra teoría de Buck (1980) propone una posible explicación trigonométrica ya que los valores de la columna
(b/c)2 se pueden interpretar como el cuadrado de la cosecante del ángulo B,
y las filas se ordenan por estos ángulos en incrementos de aproximadamente un grado.
Se basa en que:
Cosecante (B) =
c /b
que nos indica el grado del ángulo B.
Esto explica el orden de la tabla, ya que esta está ordenada por valores del ángulo B, que van desde el ángulo
45° 14' 23" (fila 1) hasta el
58° 06' 33" (fila 15).
Parece ser que es una tabla de ternas pitagóricas de todos los ángulos que van desde
45° hasta
60°
Friberg plantea la posibilidad de que los datos en ella encerrados correspondan a un triángulo rectángulo "normalizado", entendiendo por tal aquel que se obtiene dividiendo la longitud a, b, c de los lados de un
triángulo rectángulo por la longitud de uno de sus catetos (por ejemplo, b).
Desde el planteamiento de la construcción del triángulo rectángulo normalizado, se ha podido llegar a postular el hecho de que los valores presentados en la tablilla Plimpton no respondan tan sólo al hecho de constituir
triadas pitagóricas, sino que su funcionalidad se basa en servir de referencia para que el maestro de escribas, a partir de una serie de valores de una incógnita x (p/q), pueda construir los términos necesarios (columna (c/b)
2)
para la resolución de ecuaciones cuadráticas que proponer a sus estudiantes.
En cualquier caso, está comprobado que conocían como calcular la hipotenusa de cualquier cuadrado,
como ya vimos en la YALE #7289, y por tanto el cálculo de la hipotenusa de cualquier triángulo rectángulo isósceles.
Tablilla YALE #7289.

La tablilla muestra la imagen de un cuadrado, donde se han dibujado las hipotenusas.
En uno de los lados del cuadrado se indica la cifra 30.
Se supone que es la tablilla de un alumno, con un ejercicio para calcular la hipotenusa. de un cuadrado de lado 30.
El alumno primero escribe el valor de la hipotesuma en un cuadrado de lado 1 que es
√2
, equivalente a la inscripción
1;24,51,10. Este es un valor que los sumerios conocían y que se ha
descubierto en varias tablillas de constantes.
Y luego multiplica ambos números obteniendo
42;25,35 que es el valor de la hipotenusa buscada.
F Ir al inicio de la página
Cálculo de áreas
Los sumerios sabían como calcular diferentes áreas geométricas
En varias de las tablillas encontradas, principalmente las que están en la Yale Babylonian Collection (YBC) se encuentran algunos hallazgos matemáticos interesantes.
Cálculo área de trapezoide
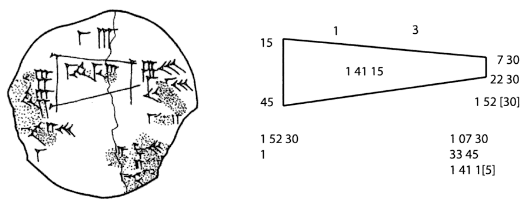
Tablilla YALE #7290.


La tablilla YBC 7290, contiene un ejercicio de escritura estudiantil en el que se registró el área de un trapezoide designado.
Trasladando el texto de izquierda a derecha, la base del trapecio se da como 2; 20 .
También se citan los dos lados del trapecio como 2;20 y la base restante 2;00.
El resultado del área calculada es de 5; 03, 20
La fórmula utilizada por es estudiante para aproximar un área trapezoidal que se empleó aquí fue:
El área es igual a la media de los lados multiplicada por la media de las bases
El reverso de la tableta YBC 7290 contiene un diagrama de un trapecio y está desprovisto de texto numérico.
Tal vez el estudiante escriba estaba simplemente practicando el dibujo de la figura.
Hay otras muchas otras tablillas con cálculos parecidos de trapezoides como la YBC 11126, de la Yale Babylonian Collection, fechada entre 1900 y 1600 AC. o
la ASHM 1922-0168 del Ashmolean, fechada en la misma época.
Cálculo del área del círculo
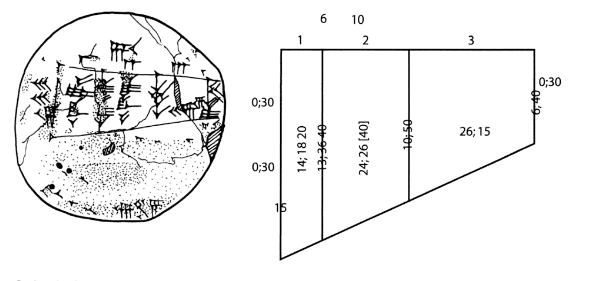
Tablilla YALE #11120.

La tablilla YBC 11120 contiene el dibujo de un círculo y el cálculo de su área.
La inscripción cuneiforme da el número sexagesimal 1;30, que representa la medida de la circunferencia del círculo dado. (1,5 en notación decimal)
El número a la derecha, 2;15 que es el cuadrado de la circunferencia:
(1;30)2 = 2; 15
Para calcular del área de un círculo, los sumerios emplearon la circunferencia como un factor, en vez del radio o el diámetro como hacemos nosotros.
Su fórmula para el área de un círculo era:
AREA = (;05) · (circunferencia)2
Donde
;05 es una constante que ellos utilizaban y que es equivalente a nuestra fracción
1/12, que se puede asimilar a
1/4 de π.
Esto indica que usaban el
3; como aproximación a
π.
En otras tablillas se ha encontrado una aproximación de
π como
3;7,30 que equivale a nuestro
3+1/8 = 3,125 , aproximación más exacta, que es considerada
como el valor racional de
π [7]
El resultado del cálculo es:
0;11,15 equivale a nuestra fracción 3/16.
Tablilla YALE #7302


La tablilla YBC 7302 muestra una circunferencia en la que aparecen el número "3;" en la parte
superior el ";45" en el interior y el "9;" en la parte derecha .
Su interpretación, sería la siguiente: el área del círculo es ";45"
Como ya hemos mencionado los escribas usaban la formula:
AREA = (;05) · (circunferencia)2
AREA = (;05) · (3)2 = ;45
De esta forma, se tiene que "3" es la longitud de la circunferencia (y por eso parece al lado de ésta), "9" es su cuadrado y por tanto el área es
0;05·9 =
0;45, valor que por representar el área aparece dentro de la circunferencia.
Cálculo área del triángulo
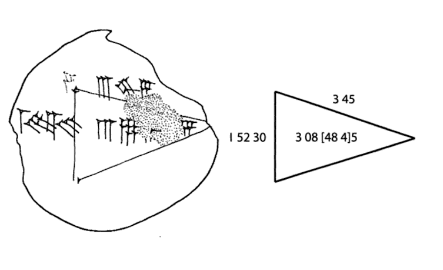
En la tableta ASHM 1931-91 datada (1900-1600 AC) que se encuentra en el Museo Ashmolean de Oxford, se puede ver :
El estudiante que escribió ASHM 1931-91 quería resolver el área de un triángulo rectángulo conociendo sus dos catetos. Un cateto es 3;45 y el otro
es 1;52,30 .
La respuesta correcta hubiera sido 0;30 x 1;52,30 x 3;45 = 3;30,56,15, pero se ha visto que se equivocó al calcularlo
ya que movió incorrectamente un número [9] y obtuvo 3;08,48,45
Volviendo a la famosa tablilla YBC7289, en su reverso, encontramos:
Es la solución a un problema parecido con un triángulo de lados 3-4-5
Cálculo del área del polígonos regulares
En 1936 se hallaron en Susa , un grupo de tablillas con resultados geométricos significativos.
Una tablilla compara las áreas y los cuadrados de las lados de los polígonos regulares de tres a siete lados. Donde se indica:
Área del pentágono/(lado)2
= 1;40
Área del hexágono/(lado)2
= 2;37,30
Área del heptágono/(lado)2
= 3;41
Nosotros por geometría sabemos que :
Área del polígono regular/(lado)2
=
N/4 · tang (180/N)
. Siendo N el número de lados del polígono.
Con lo que comprobamos que las constantes calculadas en la tablilla da errores entre 3 y 6 centésimas.
También en esta tablilla compara el perímetro de un exágono y de la circuferecia que lo circunscribe:
Perímetro del hexágono/Circunferencia
= 0;57,36
Nosotros por geometría sabemos que :
Perímetro del hexágono/Circunferencia
=
3 /π
Esto nos indica que conocían un valor de
π = 3+1/8 , o sea 3,125
F Ir al inicio de la página
Solucionar Ecuaciones cuadradas
Los matemáticos babilónicos antiguos entendían las ecuaciones de segundo grado como problemas para los lados y áreas de rectángulos y cuadrados y por consiguiente,
sus métodos para la solución de ecuaciones cuadráticas se basaban en manipulaciones con rectángulos y cuadrados en términos lados y áreas.
En el British Museum se conserva la tableta BM 13901, que originalmente contenía 24 problemas de equaciones cuadradas, algunos estan dañados, pero los que se conservan nos
dan información de como los resolvían.
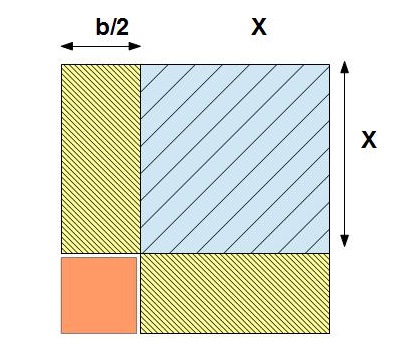
El primer problema de la tablilla dice "Yo añado juntos UNO al lado de mi cuadrado y tengo un area de 0;45"
Esto se puede interpretar como una ecuación del segundo grado del tipo:
x2 + bx = c
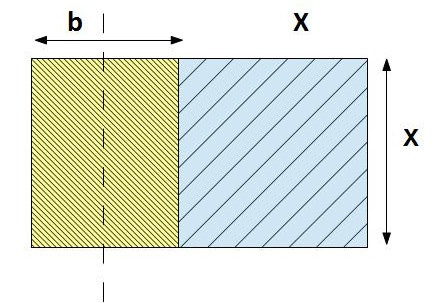
Miremos el dibujo de la derecha, observamos un cuadrado de lado X, al que hemos añadido un segmento b, en uno de sus lados, obteniendo un rectángulo.
Si suponemos que el área del rectángulo mayor (área amarilla y azul) es igual a C, y que es igual a la multiplicaciónde ambos lados tendremos que:
x · (x+b) = c
x2 + bx = c
En el problema de la tablilla tenían que
b = 1; y que
c = 0;45
Como lo resolvieron. Mirando los números que van apareciendo en la tablilla detectamos las siguientes fases en la resolución del problema:
Tomaban b que es 1; y calculaban su mitad que es 0;30
Lo elevaban al cuadrado o sea (b/2)2 y obtenían 0;15
Hacían la suma de c+(b/2)2 que es 0;45 + 0;15 = 1;
obtenían su raiz cuadrada , o sea 1;
y le restaban (b/2) , o sea 1; - 0;30 = 0;30
Obteniendo la respuesta. El lado del cuadrado es 0;30
¿Porque lo hacían así?
Esto se puede interpretar como un problema geométrico:
El área C del dibujo anterior, podemos representarla dentro de un gran cuadrado de lados (x+b/2)
En este cuadrado hemos mantenido el área C (zona amarilla y azul), y hay una zona marrón adicional necesaria para crear el cuadrado grande.
Para calcula X ahora es sencillo. Se calcula el área del cuadrado grande. Esto es sumar el área C con el cuadrado de lado (b/2).
Como conocemos C y b , esto no es problema
Obtenemos el valor del lado del cuadrado grande, sacando la raiz cuadrada al área obtenida
Como sabemos que el lado también es igual a x + (b/2) , tenemos que el valor X será el valor del lado restándole b/2 .
F Ir al inicio de la página
Solucionar Ecuaciones cúbicas
La Solucion de " x3= a " fue lograda usando tablas e interpolaciones.
La mezcla de cubos y cuadrados "x3+x2= a" también fue solucionada usando las tablas y las interpolaciones
La ecuación cubica general "ax3 + bx2 + cx = d" puede ser reducida a su forma normal
"y3 + ey2 = g (ya comentada)
F Ir al inicio de la página
Solucionar sistemas lineares.
Lo solucionaban reduciendo el problema de dos variables a una m en un proceso de eliminación, en cierta forma parecido a la Elimininación Gaussiana
Más Geometría
Habia varias para calcular el volumen de un tronco
Hay muchos problemas geométricos en los textos del cuneiformes. Por ejemplo, los sumerios estaban enterados que
- La altura de un triángulo isósceles bisecciona la base.
- Un ángulo inscrito en un semicírculo es un angulo recto. (Thales)
F Ir al inicio de la página
Material:
Traducción, ampliación , corrección y adaptación del texto : D. Allen "Babylonian Matematics". History Deparment. Texas A&M University.
Referencias:
[1] D. Fowler David y E.Robson. "Square Root Approximations in Old Babylonian Mathematics". University Warwich & University Oxford. Historia Mathematica 25 (1998), 366–378.
[2] O. Neugebauer y A. Sachs. "Textos Cuneiformes Matemáticos". American Oriental Series. Vol 29. American Oriental Society New Haven, (1945)
[3] E. M. Bruins. En Plimpton 322, "Números de Pitágoras en matemáticas babilónicas". Afdeling Naturkunde, Proc. 52 (149), 629-632.
[4] O. Neugebauer. Mathematische Keilschrift-Text. 1935. Reedicion - Ed. Springer. ISBN 978-3-642-67893-6
[5] E. Robson. "Neither Sherlock Holmes nor Babylon: A Reassessment of Plimpton 322" Historia Mathematica 28 (2001).
F. Swetz "Mathematical Treasure: Old Babylonian Area Calculation". Convergence. Mathematical Association of America (2014)
J. Friberg "A Remarkable Collection of Babylonian Mathematical Texts" - Ed Springer. (2007)
[7] M. Shetty. "Geometric Estimation of Value of Pi" (2012)
[8] T. Philips. "Old Babylonian Multiplication and Reciprocal Tables"
[9] V. Katz- The Mathematics of Egypt, Mesopotamia, China, India and Islam". Princetown University. (2007)